A táncoló matematikus: interjú a BME TTK Bolyai-ösztöndíjas kutatójával

Pete Gábor, a Természettudományi Kar Matematika Intézetén belül működő Sztochasztika Tanszék docense is egyike azon műegyetemi oktatóknak, akik idén Bolyai-ösztöndíjban részesültek.

A fiatal kutatóval a díj alkalmából beszélgettünk a valószínűségszámításról, a kortárs táncról, illetve ezek összefüggéseiről.

Mit jelent az Ön számára a Bolyai-ösztöndíj?

Pete Gábor: Örülök nagyon a Bolyainak. Két évvel ezelőtt jöttem vissza Magyarországra, előtte Észak-Amerikában végeztem PhD tanulmányokat Berkeley-ben. Kutattam Seattle-ben a Microsoft Researchnél, ahol a század egyik legnagyobb valószínűségszámítással foglalkozó matematikusával, Oded Schrammal dolgozhattam együtt. Jártam a Torontói Egyetemen is. Jelenleg az MTA Rényi Alfréd Matematikai Kutatóintézetében végzem kutatásaim egy részét, a Bolyai-ösztöndíjas kutatási, illetve oktatói munkám színhelye azonban továbbra is a BME. Megérkezésünkkor még Marie-Curie ösztöndíjat kaptam. Ebből a díjból ki lehet fizetni a gyerekek bölcsődéjét, babysitterét, így lehetőségem lesz nappal is dolgozni. A díj ezen felül számomra a beilleszkedés tudatosításában is fontos szerepet játszik.

Az Ön kutatási területe, a sztochasztika a sejtés, találgatás művészetét jelentette a görögöknél, sokak számára azonban e fogalom mai jelentése is ismeretlen.

Pete Gábor: A sztochasztikába nemcsak a szigorúan vett valószínűségszámítás tartozik bele, hanem egyéb modellek is. Wigner Jenő például egy nagy atommagot akart megérteni, a sok elektron együttes állapota azonban túl bonyolult volt ahhoz, hogy pontosan leírja, ezért azt egy véletlen modellel helyettesítette, s ebből születtek a véletlen mátrixok. Vagy például a newtoni mechanikában nincs szerepe a véletlennek, mégis, a rengeteg részecske együttes mozgását vizsgáló termodinamikában az entrópia (a rendezetlenség) állandó növekedése egy sztochasztikus jelenség. A bonyolult ismeretlennek valamifajta véletlennel való helyettesítése a tudomány elfogadott stratégiája. Ezután a valószínűségszámítás feladata, hogy a véletlen modell viselkedését egzakt tételekkel leírja. Igaz, hogy a fizikusok számára sokszor elég, ha számítógépen szimulálva látják a véletlen rendszer tipikus viselkedését, de matematikusként a sejtés bizonyítást vár, hiszen nincs olyan, hogy egy tétel nagy valószínűséggel igaz, én bizonyítást szeretnék, hiszen az mutatja a jelenség igazi megértését. Az mondjuk jó a szimulációkban, hogy általuk könnyebben érzi az ember, hogy nem teljesen absztrakt, hanem a valóságban létező jelenségeket vizsgál, és ellenőrizhetjük velük sejtéseink jogosságát.

Ön hisz a véletlenben?

Pete Gábor: Nem tudom, hogy van-e véletlen. Olyan bonyolult folyamatok vannak, hogy azokat teljesen racionálisan nem tudom megérteni. Ezeket hívhatjuk akár véletleneknek is. A fontosabb racionális döntéseim előtt egy kicsit gondolkodom „valszámosan”, például pénzügyi döntések előtt. A véletlen létére, mint filozófiai kérdésre, leginkább empirikus választ adnék: a tapasztalat azt mutatja, hogy véletlen van, és nem is lehet megszüntetni.

Mely területek adják kutatásainak főbb területeit?

Pete Gábor: Kutatásaim egyik területe a kétdimenziós (síkbeli) sztochasztikus (véletlen) folyamatok. Itt síkbeli véletlen folyamatokat vizsgálunk, ezeket a legegyszerűbben két példával lehet elmagyarázni: az első a bolyongás a négyzetrácson (azaz mindig 1/4-1/4 valószínűségekkel valamelyik szomszédos csúcsra lépünk), illetve ennek skálalimesze (amikor messziről nézzük a folyamatot hunyorítva) a Brown-mozgás az euklideszi síkban, egy nagyon cikkcakkos folytonos véletlen görbe, ami a hőterjedéstől kezdve a pénzügyi matematikáig sok mindennek az alapja. A második a perkoláció a négyzetrácson, ami azt jelenti, hogy a rács minden élét egymástól függetlenül valamekkora (p) valószínűséggel megtartjuk, 1-p valószínűséggel kitöröljük, és a kapott véletlen gráf összefüggő komponenseit, más szóval fürtjeit vizsgáljuk. Itt van egy fázisátmenet: ha p kicsi, akkor csak kicsi fürtök vannak, ha pedig p közel van 1-hez, akkor van végtelen fürt is. A legérdekesebb jelenségek a két viselkedést elválasztó kritikus pc értéknél figyelhetők meg: ezt hívják kritikus perkolációnak, én leginkább ilyen kritikus jelenségekkel foglalkozom.

Az egyik fontos kritikus jelenség, hogy a kritikus perkolációnak is van egy gyönyörű skálalimesze (mint az első példában a Brown-mozgás): például a nagy fürtök határai 7/4 dimenziós véletlen fraktálok, amik átlagban forgásszimmetrikusak: nem látszik rajtuk, hogyan állt a négyzetrács.

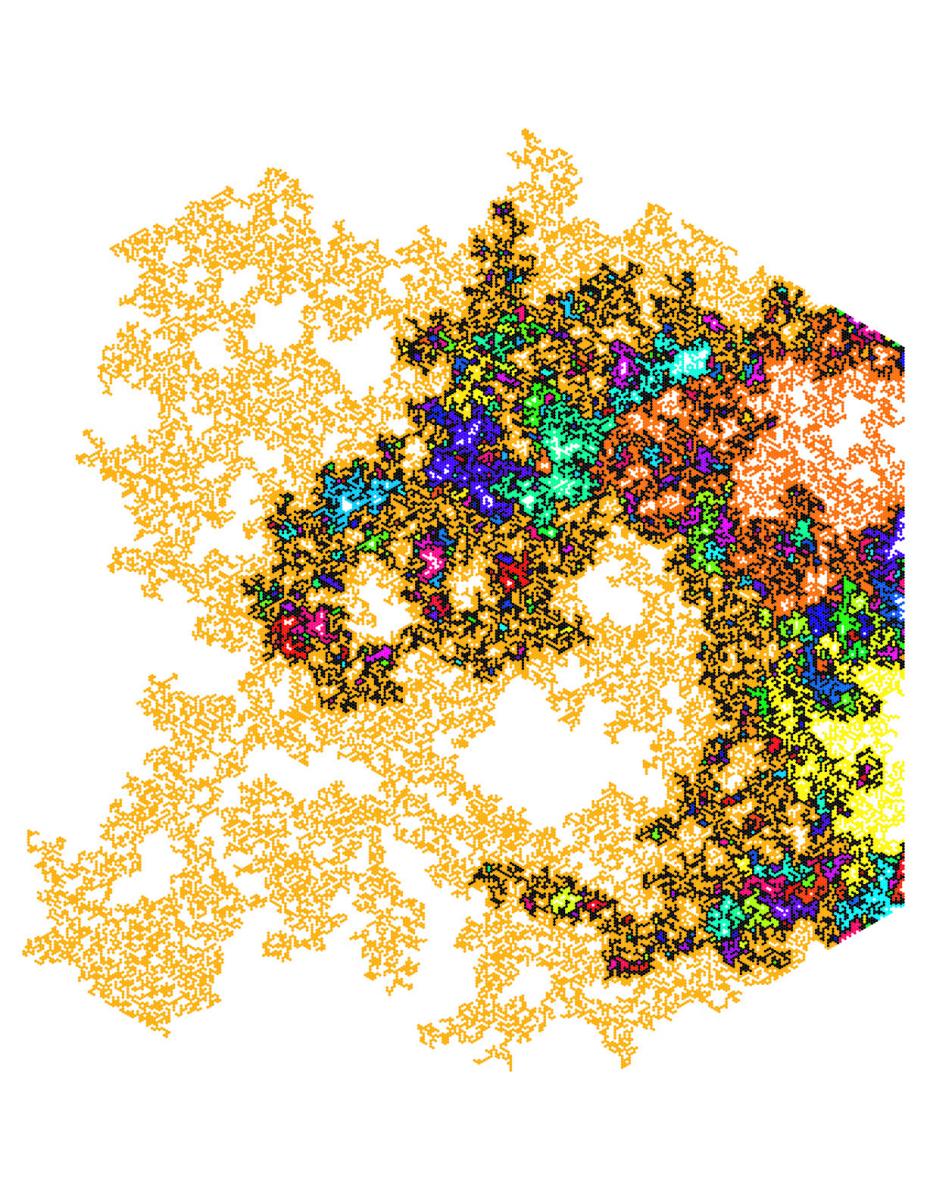
Egy véletlen fraktál: feketével egy kritikus perkoláció nagy fürtje, színessel a vele szomszédos fürtök

A honlapján a publikációs listájával azonos terjedelmű performance listát találni. A matematika mellett a tánc is hasonlóan fontos szerepet játszik az életében?

Pete Gábor: A kutatás-tanítás-család hármasa mellett mostanában kevesebb időm jut a táncra. Előadást talán öt éve nem csináltam, de azért nagyon szép és fontos elfoglaltságnak tartom. A testünkben információkkal rendelkezünk a világról, ehhez a tánc különleges médium, a táncos a testével alkot, a néző pedig a testével nézi azt. A jó néző úgy fogadja be a táncot, mintha ő csinálná. Nagyon fizikai dolog, mégis fontos érzelmi és intellektuális jelentése lehet.

Melyik volt előbb, a matek vagy a tánc?

Pete Gábor: A matek óvoda óta megvan. Emlékszem az érzésre, amikor gyerekként filcből készült színes bigyókat különböző szempontok szerint rendszerezni kellett. Ez volt az absztrahálás; ezt a szót akkor még persze nem ismertem, de az nagyon tetszett, hogy a lényegtelen dolgokat el kell felejteni, és a lényegesekre koncentrálni. A tánc később jött, 23 évesen éltem át egy személyes krízist, erőltettem a matekot, de az nem segített. Akkor jött a nővérem, aki táncterápiával foglalkozik, és rávett, hogy táncoljak. Boldogabb vagyok, ha táncolok, olyankor sokszor a matek is jobban megy.

Mi a kapocs a kortárs tánc és a matematika között?

Pete Gábor: Mi, matematikusok elméleti konstrukcióinkban saját esztétikai megérzéseinket követjük abban, hogy merre menjen a matematika, mégis sok mindent elmondunk a fizikai valóságról. Az, hogy egy ilyen intellektuális játék, mint a matematika, miért olyan fontos a fizikai valóság számára, illetve hogy a teljesen a fizikai világban lévő tánc miért olyan fontos intellektuálisan, nos, itt látok sok párhuzamos vonást. Az improvizációnak is lehet némi köze mindkettőhöz: a jó improvizációnak és a jó matematikai kutatásnak sem az előre megtanult panelek rakosgatása a lényege, hanem az intuíció.

Mely céljait látja valószínűsíthetően megvalósíthatóknak?

Pete Gábor: Az ösztöndíj végére szeretném elkészíteni az MTA doktorimat, és befejezni a Probability and geometry on groups című könyvemet, ami inkább a másik kutatási területemről szól, ahol az alapgráf nem egy síkrács, hanem valami ún. nemtriviális geometriájú struktúra. Emellett szeretnék iskolát alapítani arra a tudásra, amit külföldről hazahoztam és itthon nincs igazán jelen. A matematikus hallgatókon kívül a fizikusok is nagyon jók, most két MSc-s hallgatóm van, reméljük lesz OTDK mindkettőjük esetében, és Kertész János professzorral (BME TTK Elméleti Fizika Tanszék) megosztva van egy PhD hallgatóm is. Folytatni akarom az elmúlt években megkezdett kutatásaimat is, annak vizsgálatát, hogy a kritikus rendszerek makroszkopikus struktúrái hogyan változnak dinamika hatására, mennyire zajérzékenyek, vagy például az anyagok mágnesezhetősége hogyan alakul ki a kritikus hőmérséklet környékén.

Hol alkalmazhatók ezek a kutatások?

Pete Gábor: A síkbeli dolgok az elméleti fizikában, a konform-térelméletben, a bonyolultabb gráfokon való véletlen folyamatok pedig modellezhetik a vírusok vagy gazdasági információk terjedését hálózatokban, vagy szociológiai szempontokból is érdekesek lehetnek.
 

- Keszler P  -

Fotó: Pintér Erik